Anh em lập trình viên chắc không xa lạ gì với các thuật toán sắp xếp như Bubble Sort, Selection Sort, Quick Sort,… hầu hết các thuật toán sắp xếp cơ bản đều dựa trên việc so sánh (based sorting). Trong khoa học máy tính, có rất nhiều thuật toán sắp xếp khác nhau mà không dựa trên việc so sánh giá trị trực tiếp của các phần tử, hôm nay chúng ta cùng tìm hiểu một thuật toán sắp xếp thuộc dạng sắp xếp theo cơ số là Radix Sort và cách triển khai nó trong ngôn ngữ lập trình Javascript nhé.
Thuật toán Radix Sort
Radix Sort – sắp xếp theo cơ số là một thuật toán dựa trên ý tưởng rằng nếu một dãy số đã được sắp xếp hoàn chỉnh thì từng chữ số cũng sẽ được sắp xếp hoàn chỉnh dựa trên giá trị của các chữ số đó. Từ “radix” trong toán học có nghĩa là cơ số, là số các chữ số của hệ đếm bao gồm cả số 0. Ví dụ như số chúng ta sử dụng hàng ngày là hệ thập phân hay hệ cơ số 10, sẽ dùng 10 chữ số từ 0-9 để biểu diễn số trong hệ. Hay với hệ nhị phân cơ số 2 thì sẽ chỉ sử dụng 2 chữ số 0 và 1 để biểu diễn mọi số trong hệ.
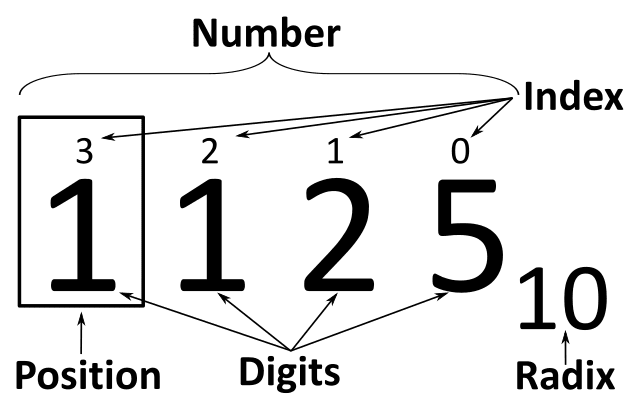

Nội dung thuật toán
Để hiểu được nội dung thuật toán, chúng ta cùng thực hiện sắp xếp mảng số sau bằng thuật toán Radix Sort (các số được biểu diễn trong hệ thập phân).
[48, 618, 836, 992 ,22, 215, 1995, 1239]
Với mỗi số trong hệ thập phân chúng ta có giá trị chữ số của từng hàng dựa theo vị trí, ví dụ 1293 thì 3 là hàng đơn vị, 9 là hàng chục, 2 là hàng trăm và 1 là hàng nghìn, … Với những số có ít chữ số hơn thì các hàng sau được hiểu có chữ số là 0, ví dụ 48 sẽ có chữ số hàng trăm và hàng nghìn đều là 0. Một cách khác chúng ta có thể biểu mảng số trên theo dạng dưới đây để tất cả các phần tử đều có cùng 4 chữ số.
[0048, 0618, 0836, 0992 ,0022, 0215, 1995, 1239]
Đầu tiên hãy chú ý vào các chữ số ở Hàng Đơn Vị, chúng ta sẽ có thể chia các phần tử trên thành các nhóm tương ứng:
- [0992, 0022] => nhóm có chữ số tận cùng là 2
- [0215, 1995] => 5
- [0836] => 6
- [0048, 0618] => 8
- [1239] => 9
Sau khi chia nhóm theo hàng đơn vị, thứ tự các phần tử trong mảng sẽ như sau:
[0992, 0022, 0215, 1995, 0836, 0048, 0618, 1239]
Lưu ý ở đây là việc chia nhóm phải giữ nguyên vị trí của các số trong nhóm theo mảng đầu vào. Ví dụ trong nhóm 2, số 0992 phải nằm trước số 0022 theo như ban đầu trong mảng cũ.
Đến đây chúng ta thực hiện lặp lại thao tác trên với lần lượt từ hàng chục, hàng trăm và hàng nghìn. Kết quả từng bước sẽ như dưới đây:
Với Hàng chục, ta có các nhóm:
- [0618, 0215] => nhóm có chữ số hàng chục là 1
- [0022] => nhóm 2
- [0836, 1239] => nhóm 3
- [0048] => nhóm 4
- [0992, 1995] => nhóm 9
Mảng sau khi sắp xếp:
[0618, 0215, 0022, 0836, 1239, 0048, 0992, 1995]
Với Hàng Trăm, ta có các nhóm:
- [0022, 0048] => nhóm có chữ số hàng trăm là 0
- [0215, 1239] => nhóm 2
- [0618] => nhóm 6
- [0836] => nhóm 8
- [0992, 1995] => nhóm 9
Mảng sau khi sắp xếp:
[0022, 0048, 0215, 1239, 0618, 0836, 0992, 1995]
Cuối cùng với Hàng Nghìn, ta có các nhóm:
- [0022, 0048, 0215, 0618, 0836, 0992] => nhóm có chữ số hàng nghìn là 0
- [1239, 1995] => nhóm 1
Mảng sau khi sắp xếp:
[0022, 0048, 0215, 0618, 0836, 0992, 1239, 1995]
Hay kết quả của mảng sau khi sắp xếp thành công sẽ là:
[22, 48, 215, 618, 836, 992, 1239, 1995]
Thuật toán Radix Sort có thể dễ dàng áp dụng tương tự trong các hệ cơ số khác, dưới đây là một ví dụ trong hệ nhị phân
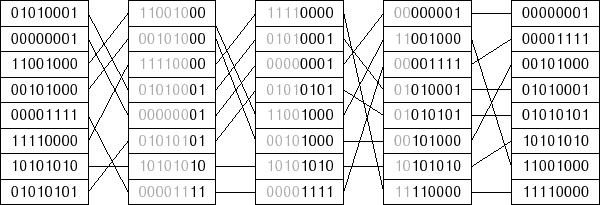

Triển khai thuật toán với JavaScript
Để thực hiện việc sắp xếp, trước tiên chúng ta có 1 số function bổ trợ cho việc tính toán gồm:
nhomTungHang: function thực hiện việc chia nhóm theo từng đơn vị hàng
//array: mảng đầu vào đã sắp xếp từ bước trướ //index sẽ là chỉ mục của hàng (hàng đơn vị, hàng chục, hàng trăm, ....) function nhomTungHang(array, index) { //cơ số sử dụng - với hệ thập phân => giá trị = 10 const BASE = 10; const modded = 10 ** (index + 1); const divided = 10 ** index; const buckets = new Array(BASE).fill(null).map(() => []); // array.forEach((element) => { if (element < divided) { //trường hợp không có giá trị hàng => gán vào nhóm 0 buckets[0].push(element); } else { //gán số vào nhóm tương ứng const currentDigit = Math.floor((element % modded) / divided); buckets[currentDigit].push(element); } }); //trả về mảng đã được nhóm return buckets; }
laySoHang: function lấy số hàng theo phần tử lớn nhất của mảng
//array: mảng đầu vào function laySoHang(array) { Math.floor(Math.log10(Math.max(...array))) + 1; }
Triển khai phần sắp xếp
//originalArray: mảng đầu vào function sort(originalArray) { let sortedArray = [...originalArray]; //lấy ra số lượng hàng để thực hiện chạy vòng lặp const numPasses = laySoHang(sortedArray); for (let currentIndex = 0; currentIndex < numPasses; currentIndex += 1) { // với mỗi vòng lặp, phân nhóm từng hàng tương ứng const buckets = nhomTungHang(sortedArray, currentIndex); // sắp xếp lại mảng các nhóm theo thứ tự sortedArray = buckets.reduce((acc, val) => { return [...acc, ...val]; }, []); } return sortedArray; }
Xem việc làm javascript đãi ngộ tốt trên TopDev
Độ phức tạp của thuật toán
Với 1 mảng có n phần tử, trong đó phần tử lớn nhất có k chữ số, khi đó
- Số vòng lặp thực hiện sẽ là k lần
- Trong mỗi vòng lặp, các phần tử sẽ chỉ được xét đến đúng 1 lần
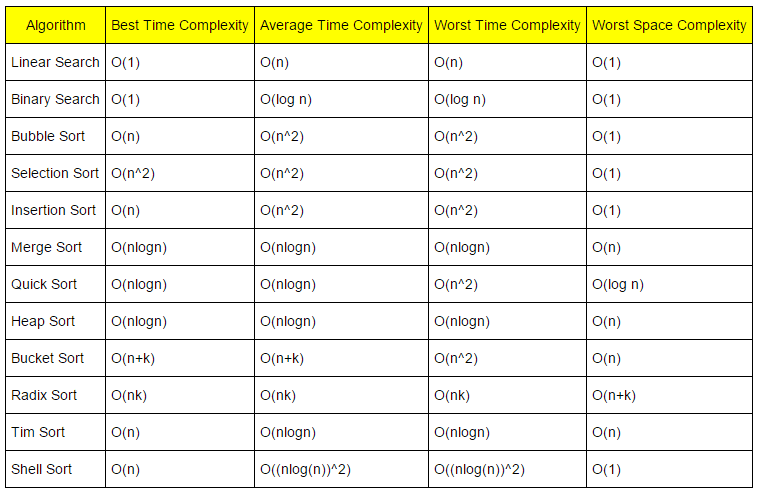
Từ đó chúng ta có số lần duyệt qua các phần tử là n * k, và số lần duyệt này là cố định trong mọi trường hợp, như vậy độ phức tạp của thuật toán này là O(n k). Nếu so sánh với các thuật toán sắp xếp cơ bản khác như Bubble Sort, Selection Sort hay Insertion Sort thì có thể xem hiệu năng của Radix Sort là khá ổn cùng tính ổn định (Stable) cao.

Kết bài
Như vậy là chúng ta đã cùng nhau tìm hiểu thuật toán sắp xếp Radix Sort và cách triển khai thuật toán này trong ngôn ngữ lập trình JavaScript. Bạn có thể cải tiến source code trên cho việc sắp xếp mảng string hay kiểu dữ liệu khác mà bạn mong muốn. Hy vọng bài viết hữu ích dành cho bạn và hẹn gặp lại trong các bài viết tiếp theo của mình.
Tác giả: Phạm Minh Khoa
Có thể bạn quan tâm:
- Thuật toán Gradient Descent
- 10 thuật toán hàng đầu dành cho lập trình viên
- Ứng dụng thuật toán và cấu trúc dữ liệu lúc đi làm
Hàng loạt việc làm IT hấp dẫn trên TopDev đang chờ bạn ứng tuyển.


















