Sử dụng thuật toán quay lui giải bài toán phân tích số bằng JavaScript

848

Thuật toán quay lui là một trong những câu hỏi thường gặp nhất khi phỏng vấn liên quan đến giải thuật trong lập trình. Trong đó bài toán phân tích số là một ví dụ thường được sử dụng để xem các ứng viên hiểu và triển khai kỹ thuật này như thế nào. Bài viết hôm nay chúng ta cùng nhau tìm hiểu về cách giải bài toán này sử dụng thuật toán quay lui với ngôn ngữ lập trình JavaScript nhé.

Bài toán phân tích số

Bài toán: Ở một quốc gia có n loại tiền gồm các mệnh giá a1, a2, …, an. Có những cách nào để lấy các tờ tiền sao cho tổng tiền của chúng là S. Trong đó mỗi mệnh giá có thể lấy được nhiều lần.

Ví dụ chúng ta có 3 loại mệnh giá 10 đ, 20 đ và 50 đ, để lấy được ra số tiền 100 đ chúng ta có thể có một số cách như là :

10 tờ 10 đ
2 tờ 50 đ
3 tờ 10 đ + 1 tờ 20 đ + 1 tờ 50 đ
…

JavaScript có thể làm được nhiều hơn bạn nghĩ!

Thuật toán quay lui

Quay lui – Backtracking là một kỹ thuật thiết kế giải thuật dựa trên giải thuật đệ quy, ý tưởng của nó là việc tìm lời giải cho từng bước một, mỗi bước sẽ chọn ra một trong số các lựa chọn khả dĩ và đệ quy. Mục tiêu của thuật toán quay lui là sẽ liệt kê hết tất cả các cấu hình có thể có, với mỗi cấu hình được xây dựng bằng cách xây dựng từng phần tử, mỗi phần tử được chọn bằng cách thử tất cả các khả năng. Vì tính chất này mà thuật toán Backtracking còn được gọi tên là phương pháp vét cạn.

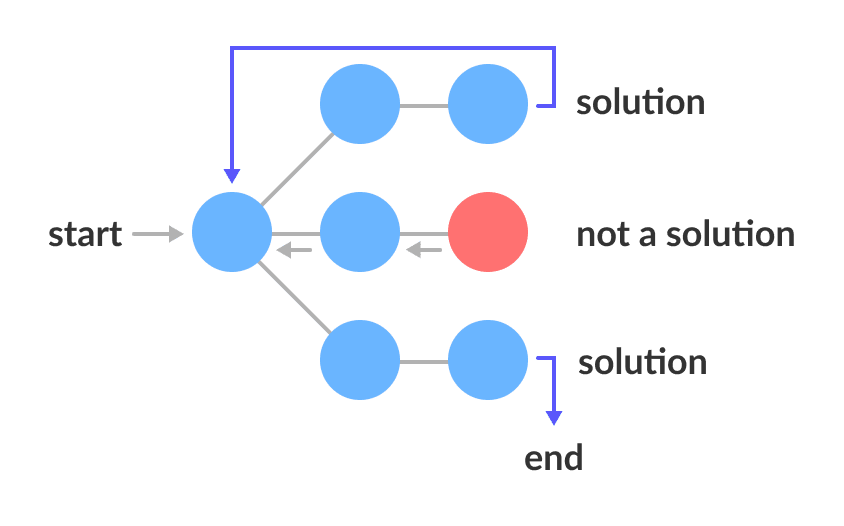
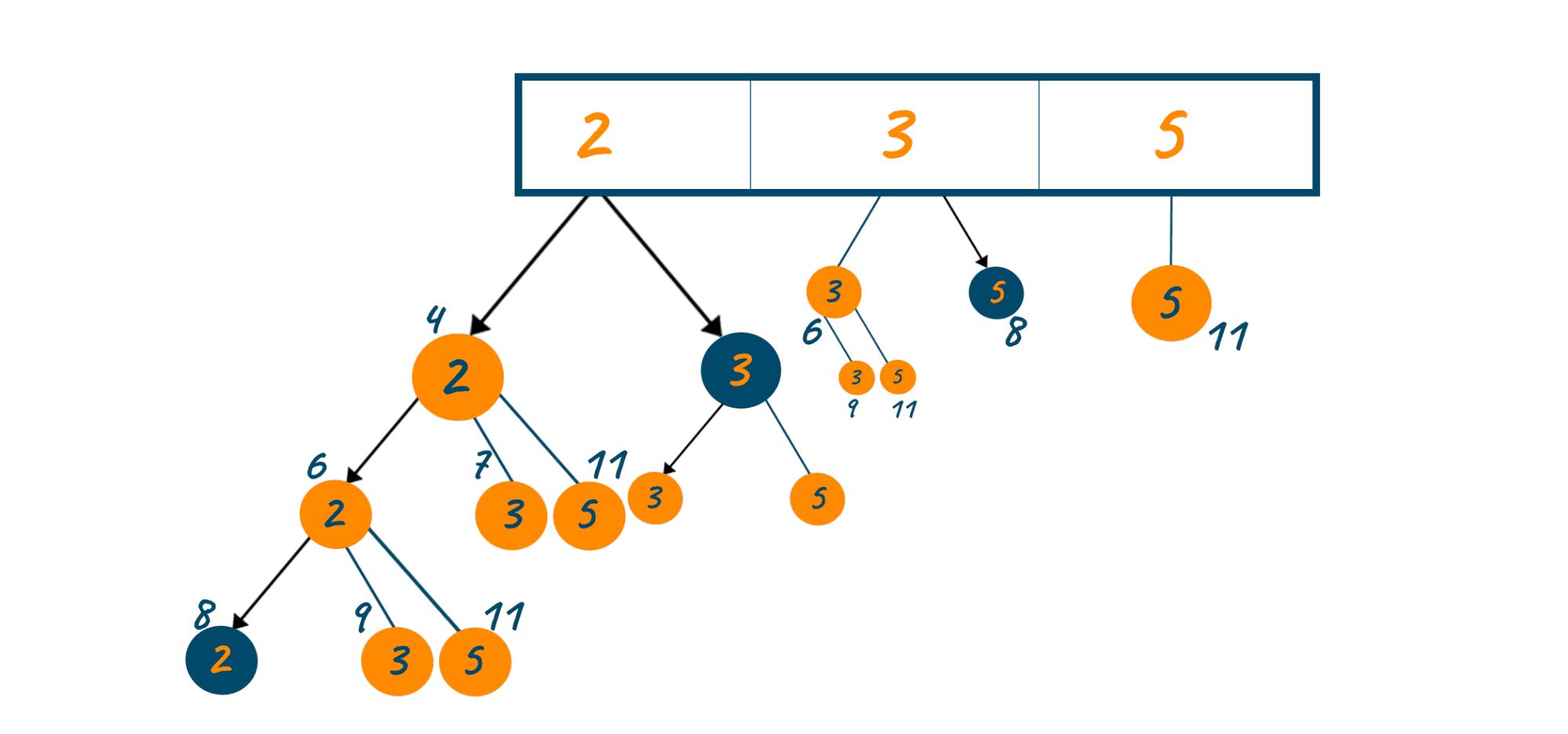
Backtracking khi triển khai, liệt kê hết các cấu hình có thể sẽ cho chúng ta một đồ thị dạng cây với giá trị của mỗi node sẽ là giá trị đạt được khi ghép các phần tử ban đầu lại với nhau. Từ đó chúng ta cũng nhận ra được bản chất của thuật toán này là một quá trình tìm kiếm theo chiều sâu DFS (Depth-First Search).

Áp dụng với bài toán phân tích số, để đưa ra được phương án đúng, chúng ta sẽ xây dựng một danh sách gồm tất cả các tập hợp có thể có khi ghép các mệnh giá tiền với nhau (lưu ý là các mệnh giá có thể lặp lại nhiều lần). Sử dụng đệ quy cho việc gọi xử lý tính toán và tạo tập hợp, điều kiện dừng đệ quy là khi tổng của tập hợp tạo ra lớn hơn hoặc bằng giá trị cần đạt. Trong mỗi lời gọi đệ quy, một vòng lặp sử dụng để duyệt qua một lượt tất cả các phần tử trong mảng mệnh giá tiền.

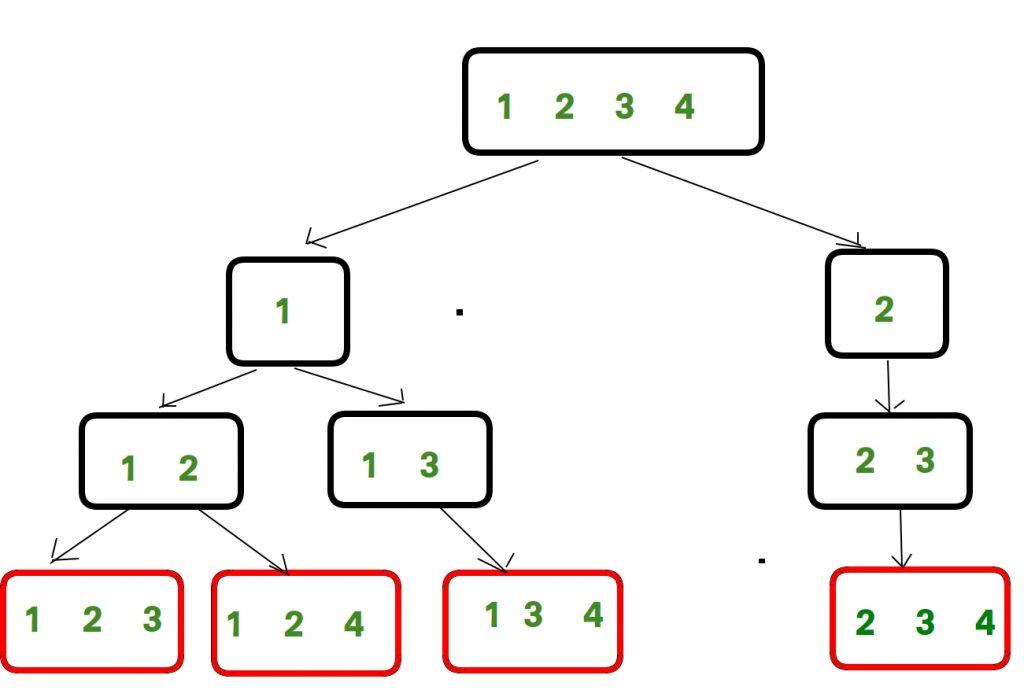
Ưu điểm của thuật toán quay lui là việc chúng ta tạo ra được tổ hợp tất cả các phương án hoàn chỉnh có thể là một lời giải, giúp tránh việc phải thử nhiều trường hợp chưa hoàn chỉnh sẽ ảnh hưởng đến thời gian chạy. Trong trường hợp tập hợp đầu vào không đổi thì việc sử dụng đệ quy có nhớ sẽ giúp chương trình đưa ra được kết quả mà không cần chạy lại thuật toán.

Tuy vậy thì nhược điểm của nó cũng chính là do sử dụng đệ quy tạo ra nhiều công việc dư thừa. Độ phức tạp của Backtracking sẽ ở cấp số mũ trong những trường hợp xấu nhất. Để cải tiến thuật toán, chúng ta có thể làm thêm một số tinh chỉnh đầu vào, ví dụ như nếu tập hợp số tất cả đều là số chẵn thì không thể cho ra tổng giá trị là lẻ; hay nếu tổng là một giá trị chẵn thì số phần tử lẻ luôn phải là mẫu số của 2,…

Tham khảo việc làm JavaScript tại Hồ Chí Minh trên TopDev

Triển khai code JavaScript

Chúng ta sẽ tạo function combinationSumRecursive cho việc gọi đệ quy với các tham số đầu vào:

candidates: mảng số đầu vào tương ứng với các mệnh giá tiền
remainingSum: giá trị tổng tiền còn lại cần đạt được với mỗi vòng đệ quy. Ban đầu sẽ chính là tổng tiền cần đạt được S
finalCombinations, currentCombination: 2 mảng lưu các giá trị kết hợp giữa các mệnh giá
startFrom: lưu chỉ số trong mảng mệnh giá cho việc duyệt

Sự khác biệt giữa encodeURI và encodeURIComponent trong JavaScript

Giải thuật được triển khai với code JavaScript như dưới đây:

function combinationSumRecursive(
  candidates,
  remainingSum,
  finalCombinations = [],
  currentCombination = [],
  startFrom = 0
) {
  if (remainingSum < 0) {
    return finalCombinations;
  }
  if (remainingSum === 0) {
    finalCombinations.push(currentCombination.slice());
    return finalCombinations;
  }
  for (
    let candidateIndex = startFrom;
    candidateIndex < candidates.length;
    candidateIndex += 1
  ) {
    const currentCandidate = candidates[candidateIndex];
    currentCombination.push(currentCandidate);
    combinationSumRecursive(
      candidates,
      remainingSum - currentCandidate,
      finalCombinations,
      currentCombination,
      candidateIndex
    );
    currentCombination.pop();
  }
  return finalCombinations;
}
export default function combinationSum(candidates, target) {
  return combinationSumRecursive(candidates, target);
}

Dễ thấy việc gọi đệ quy sẽ được dừng lại khi remainingSum < 0 (phương án bị loại) hoặc = 0 (sẽ trả về kết quả là 1 phương án đúng). Thuật toán quay lui sẽ cho ra tất cả các tổng có thể có được nhỏ hơn S, vì thế trong trường hợp yêu cầu bài toán có nhiều giá trị S đầu vào, chúng ta có thể xử lý lại code để chỉ cần chạy một lượt đệ quy dành cho giá trị S lớn nhất hay sử dụng đệ quy có nhớ.

Kết bài

Như vậy chúng ta đã cùng nhau tìm hiểu về bài toán phân tích số, cách sử dụng giải thuật quay lui để giải quyết nó cũng như triển khai code bằng ngôn ngữ lập trình JavaScript. Hy vọng qua bài viết này các bạn có thể tự tin để trả lời nếu gặp câu hỏi giải thuật đến từ nhà tuyển dụng. Hẹn gặp lại các bạn trong các bài viết tiếp theo của mình.

Tác giả: Phạm Minh Khoa

Có thể bạn quan tâm:

Hàng loạt việc làm IT hấp dẫn trên TopDev đang chờ bạn ứng tuyển..