Tim Sort là một giải thuật sắp xếp kết hợp từ Merge sort và Insertion sort, nó được thiết kế để hoạt động tốt trong nhiều trường hợp dữ liệu cần sắp xếp trong thực tế. Tim Sort được sử dụng làm giải thuật mặc định trong Python với hàm sorted() và list.sort(). Bài viết hôm nay chúng ta cùng nhau tìm hiểu về giải thuật này nhé.
Giải thuật TimSort
Tim Sort được Tim Peters triển khai lần đầu tiên vào năm 2002 để sử dụng trong ngôn ngữ lập trình Python. Theo Tim Peters, lý do ông cho ra đời giải thuật này là vì ông nghĩ rằng hầu hết các thuật toán sắp xếp hiện có đều ra đời trên lý thuyết, trong các lớp học lập trình mà không được thiết kế để sử dụng thực tế trên dữ liệu từ thế giới thực.

Trong tất cả các giải thuật sắp xếp cơ bản, thao tác chính được lặp đi lặp lại trong quá trình thực hiện là việc so sánh (compare) giữa hai phần tử với nhau và hoàn đổi vị trí (swap) nếu cần. Với những bài toán thực tế, khi kích thước của tập hợp dữ liệu cần sắp xếp lớn thì chúng ta có thể nhận thấy rằng có nhiều phân đoạn dữ liệu đã được sắp xếp sẵn từ trước. Điều này có thể là vấn đề gây ra những lần so sánh và hoán đổi một cách không cần thiết.


Ý tưởng chính đứng sau giải thuật Tim Sort này là việc tận dụng, khai thác thứ tự hiện có trong dữ liệu ban đầu nhằm giảm thiểu số lượng các bước so sánh và hoán đổi trong quá trình thực hiện giải thuật. Thuật toán này thực hiện việc chia mảng (tập hợp) ban đầu thành các mảng con nhỏ hơn gọi là chuỗi (runs); thực hiện giải thuật Insertion Sort để sắp xếp thứ tự trong các chuỗi đó; cuối cùng là thực hiện bước merge các chuỗi sử dụng Merge Sort để cho ra kết quả cuối cùng.
Để hiểu rõ hơn về ý tưởng của giải thuật này, trước hết chúng ta cùng nhắc lại một chút về Merge Sort và Insertion Sort nhé.
Nhắc lại Insertion Sort và Merge Sort
Insertion Sort hay sắp xếp chèn là một thuật toán sắp xếp đơn giản dựa trên việc so sánh tại chỗ. Nó chia mảng thành hai phần: một phần được sắp xếp và một phần chưa được sắp xếp. Quá trình chạy thuật toán sẽ thực hiện việc duyệt qua từng phần tử trong phần chưa được sắp xếp và chèn nó vào đúng vị trí trong phần đã được sắp xếp.
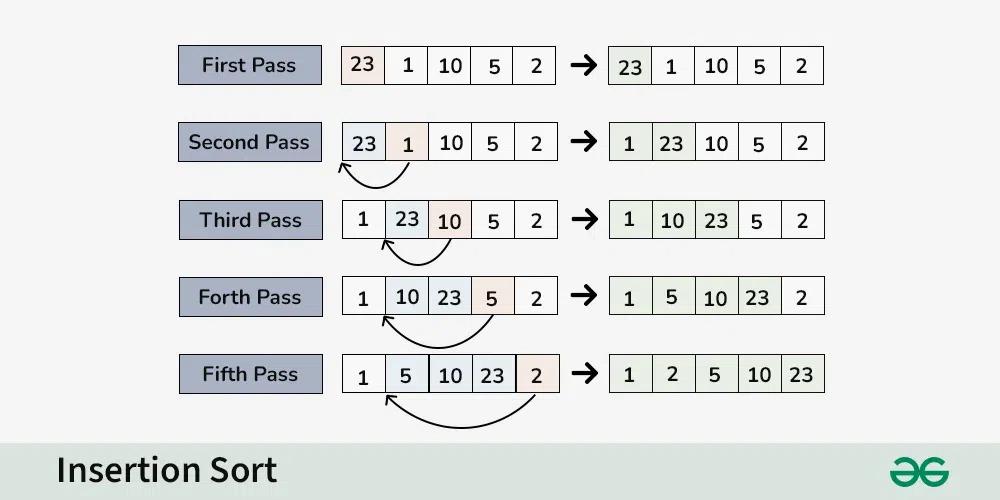

Merge Sort hay sắp xếp trộn là một thuật toán sắp xếp dựa trên kỹ thuật chia để trị (Divide and Conquer). Ý tưởng của giải thuật này bắt nguồn từ việc trộn hai danh sách đã sắp xếp thành một danh sách mới sẽ được sắp xếp.


Quá trình trộn hai danh sách đã sắp xếp sẽ được thực hiện như sau:
- So sánh hai phần tử đứng đầu hai danh sách, lấy phần tử nhỏ hơn cho vào danh sách mới
- Tiếp tục như vậy cho tới khi một trong hai danh sách là rỗng
- Khi một trong hai danh sách là rỗng thì ta lấy phần còn lại của danh sách kia cho vào cuối danh sách
Ý tưởng của Tim Sort
Chúng ta có bảng tổng hợp về độ phức tạp thời gian và bộ nhớ sử dụng giữa các giải thuật sắp xếp như dưới đây.
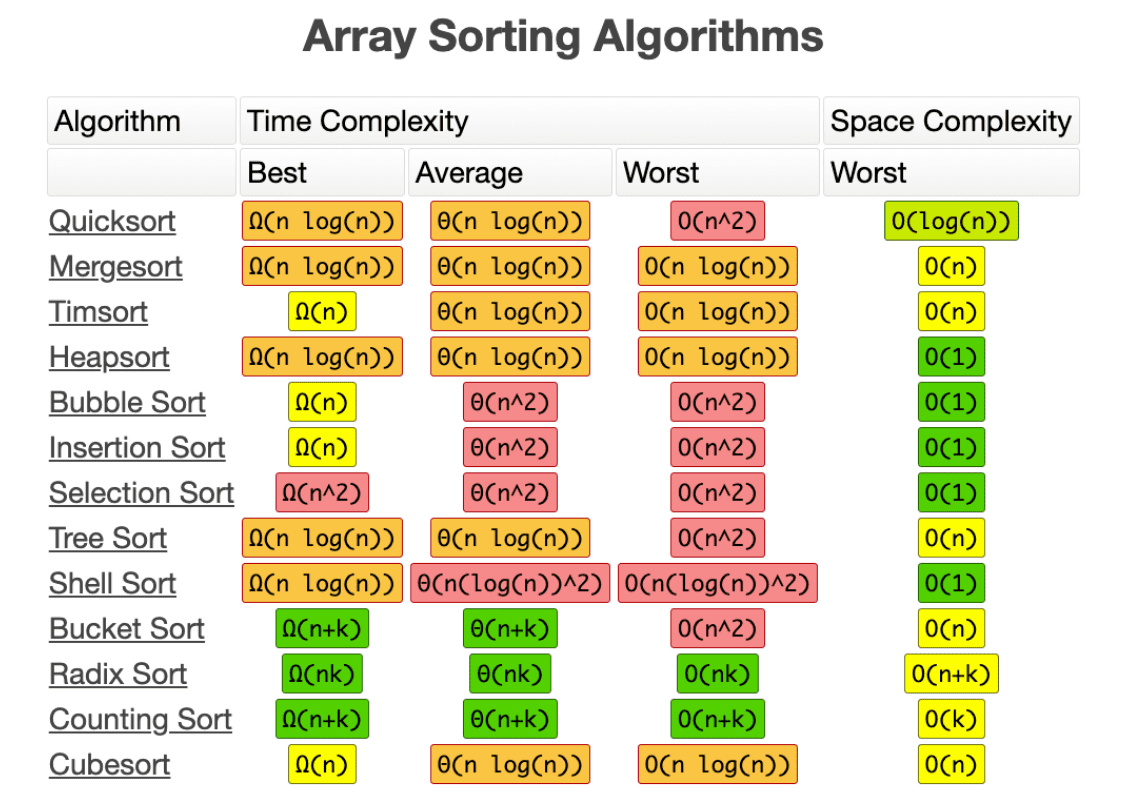

Insertion Sort là một giải thuật đơn giản, nhưng lại có một ưu điểm ở khía cạnh thời gian chạy trong trường hợp tốt nhất (best case). Điều này nói lên rằng, nếu dữ liệu cần sắp xếp vốn dĩ được “sắp xếp một phần” nào đó thì sắp xếp chèn là một lựa chọn tốt. Dĩ nhiên, Insertion Sort chỉ có thể chạy với một tập dữ liệu nhỏ, vì nếu thực hiện trên một mảng kích thước lớn thì độ phức tạp cũng sẽ tăng lên theo cấp số mũ. Tiếp theo chúng ta chú ý đến dòng Merge Sort, đây là một giải thuật có độ ổn định trong tất cả các trường hợp, nói cách khác nó không phụ thuộc vào dữ liệu đầu vào, sẽ luôn thực hiện và cho ra độ phức tạp về mặt thời gian như nhau.
Từ 2 nhận định này, Tim Sort ra đời với việc kết hợp Merge Sort và Insertion Sort nhằm tận dụng được cả tính ổn định của Merge Sort cùng tính “tốt” trong best case của Insertion Sort. Chúng ta cùng đi vào các bước cụ thể của giải thuật Tim Sort nhé.
Triển khai giải thuật Tim Sort
Bước 1: Xác định kích thước của một run
Như đã nhắc ở trên, runs là các chuỗi con có kích thước nhỏ được Tim Sort chia ra từ tập hợp ban đầu để thực hiện sắp xếp. Khuyến nghị từ Tim Sort là kích thước nhỏ nhất mà một run nên có là 32 (giá trị sẽ thường là 32, 64 – những lũy thừa của 2), cũng không nên quá lớn vì có thể làm ảnh hưởng đến hiệu quả của Insertion Sort.
Bước 2: Thực hiện chia mảng ban đầu thành các runs và thực hiện Insertion Sort trong các runs
Việc áp dụng sắp xếp chèn trên các runs có kích thước nhỏ là một lựa chọn hợp lý và tốt cho dữ liệu thực tế. Có một lưu ý rằng Tim Sort không nhất thiết chia mảng ban đầu ra thành các runs theo chỉ số (index); bạn hoàn toàn có thể chia từng cụm bất kỳ có kích thước quy định ở bước 1; điều này đặc biệt hữu ích nếu bạn biết trước sẵn có những runs mà dữ liệu cơ bản đã được sắp xếp.
Bước 3: Chạy Merge Sort để hợp nhất các runs
Sau khi các runs đã được sắp xếp, chúng ta bắt đầu hợp nhất chúng lại với nhau bằng thao tác merge trong Merge Sort. Hãy thực hiện merge các runs có chung kích thước, có nghĩa là việc merge được chạy trên toàn bộ dữ liệu cùng một lúc. Từng cặp sẽ được sắp xếp lại cho đến khi hoàn thiện được tập hợp ban đầu với thứ tự đã sắp xếp.
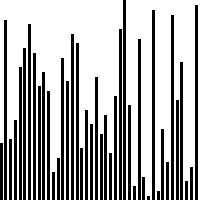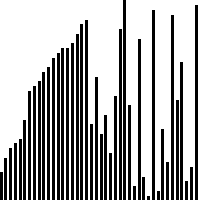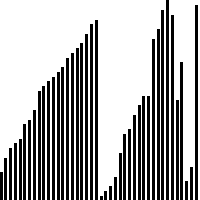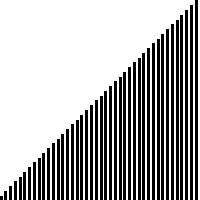
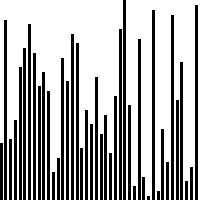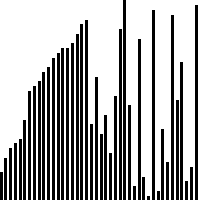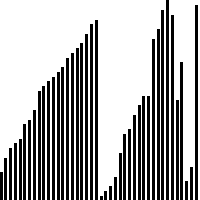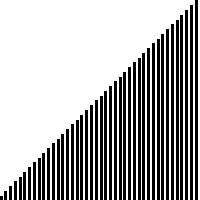
Độ phức tạp của Tim Sort về mặt thời gian so với các giải thuật khác được đánh giá rất tốt, ở mức trung bình là O(n logn) và có tính ổn định. Mặc dù vậy thì Tim Sort cũng có một nhược điểm là việc sử dụng bộ nhớ (độ phức tạp bộ nhớ) cao hơn so với một số giải thuật sắp xếp khác. Trong thực tế, Tim Sort không chỉ được sử dụng làm giải thuật sắp xếp mặc định trong Python, nó còn được Java 7 hay JavaScript và một số ngôn ngữ khác lựa chọn nhờ tính ổn định (stable) của mình.
Kết bài
Qua bài viết này, hy vọng các bạn đã hiểu rõ về giải thuật Tim Sort và lý do nó được đánh giá cao trong các ngôn ngữ lập trình ưu tiên xử lý tính toán như Python. Việc triển khai Tim Sort cũng không quá phức tạp trong tất cả các ngôn ngữ lập trình mà bạn sử dụng, vì thế hãy thử tự viết ra source code của mình để thực hành nhé. Cảm ơn các bạn đã đọc bài và hẹn gặp lại trong các bài viết tiếp theo của mình.
Tác giả: Phạm Minh Khoa
Xem thêm:
- Thuật toán Gradient Descent
- Thuật toán Quick Sort là gì?
- Các thuật toán sắp xếp phổ biến trong JavaScript
Truy cập ngay việc làm IT đãi ngộ tốt trên TopDev







