Giải bài toán về dãy con tăng dài nhất trong JavaScript

832

Trong khoa học máy tính, dãy con tăng dài nhất là một trong những bài toán quy hoạch động kinh điển và được ứng dụng rộng rãi trong việc giải quyết các bài toán về sắp xếp lịch trong thực tế. Bài viết hôm nay chúng ta cùng nhau tìm hiểu về bài toán này, về thuật toán quy hoạch động và cách triển khai nó trong ngôn ngữ lập trình JavaScript nhé.

Bài toán dãy con tăng dài nhất

Dãy con tăng dài nhất – Longest Increasing Subsequence (LIS) là một bài toán với mục đích tìm ra dãy con dài nhất có thể của một dãy cho trước, trong đó các phần tử của dãy con đó được sắp xếp theo thứ tự tăng dần. Các phần tử trong dãy con này không nhất thiết phải liền kề hoặc duy nhất.

Bài toán dãy con tăng dài nhất

Ví dụ ở hình trên, với đầu vào (input) là một mảng số gồm 8 phần tử thì đầu ra (output) mong muốn của bài toán sẽ là 2 mảng con thỏa mãn yêu cầu cùng độ dài bằng 4.

Bài toán dãy con đơn điệu tăng dài nhất có biến thể đơn giản nhất là bài toán dãy con đơn điệu giảm dài nhất và thực tế là 2 bài toán này được xem là một. Ứng dụng của bài toán này trong thực tế có rất nhiều, nhất là trong các vấn đề về sắp xếp và lập lịch. Một ví dụ nổi bật là bài toán bố trí phòng khách sạn như sau:

Yêu cầu: Có n khách cùng đặt 1 phòng khách sạn, khách i nhận phòng vào thời điểm A(i) và trả phòng ở thời điểm B(i). Hãy bố trí khách vào phòng đó sao cho phục vụ được nhiều khách nhất có thể. Lưu ý bài toán giả định chỉ có 1 phòng và có thể dễ dàng mở rộng cho nhiều phòng bằng cách sắp xếp lần lượt từng phòng.

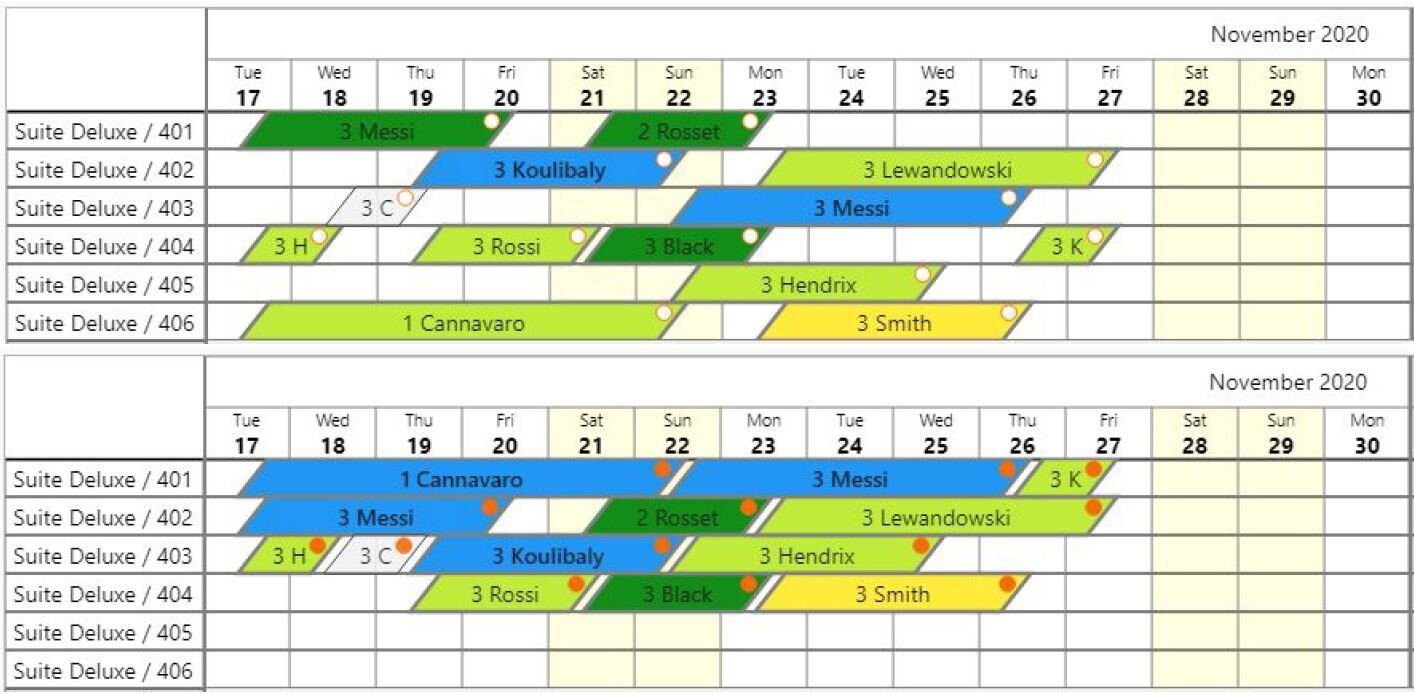
Bài toán dãy con tăng dài nhất

Chúng ta có thể chuyển yêu cầu trên về bài toán dãy con tăng dài nhất bằng cách sắp xếp các khách đặt phòng theo thời điểm kết thúc B(i) tăng dần. Khách i sẽ được sắp xếp vào phòng sau khách j khi và chỉ khi j < i và B(j) < A(i). Kết quả đầu ra từ thuật toán sẽ cho chúng ta mảng con số lượng khách tối đa có thể đặt được phòng.

Bài toán dãy con tăng dài nhất được xếp vào một trong những bài toán quy động động kinh điển, vì thế để giải bài toán này trước tiên chúng ta cùng tìm hiểu về thuật toán này nhé.

  Thuật toán tìm kiếm nội suy trong JavaScript

  Bạn biết gì về thuật toán Radix Sort trong JavaScript?

Phương pháp quy hoạch động

Quy hoạch động là một kĩ thuật thiết kế thuật toán theo kiểu chia bài toán lớn thành các bài toán con, sử dụng lời giải của các bài toán con để tìm lời giải cho bài toán ban đầu giúp chúng ta tối ưu thời gian thực hiện thuật toán. Khác với đệ quy thì quy hoạch động sẽ tính toán lời giải của các bài toán con trước và lưu vào mảng bộ nhớ; tiếp đó dùng lời giải của bài toán con trong mảng đã tính trước đó để giải bài toán theo công thức truy hồi.

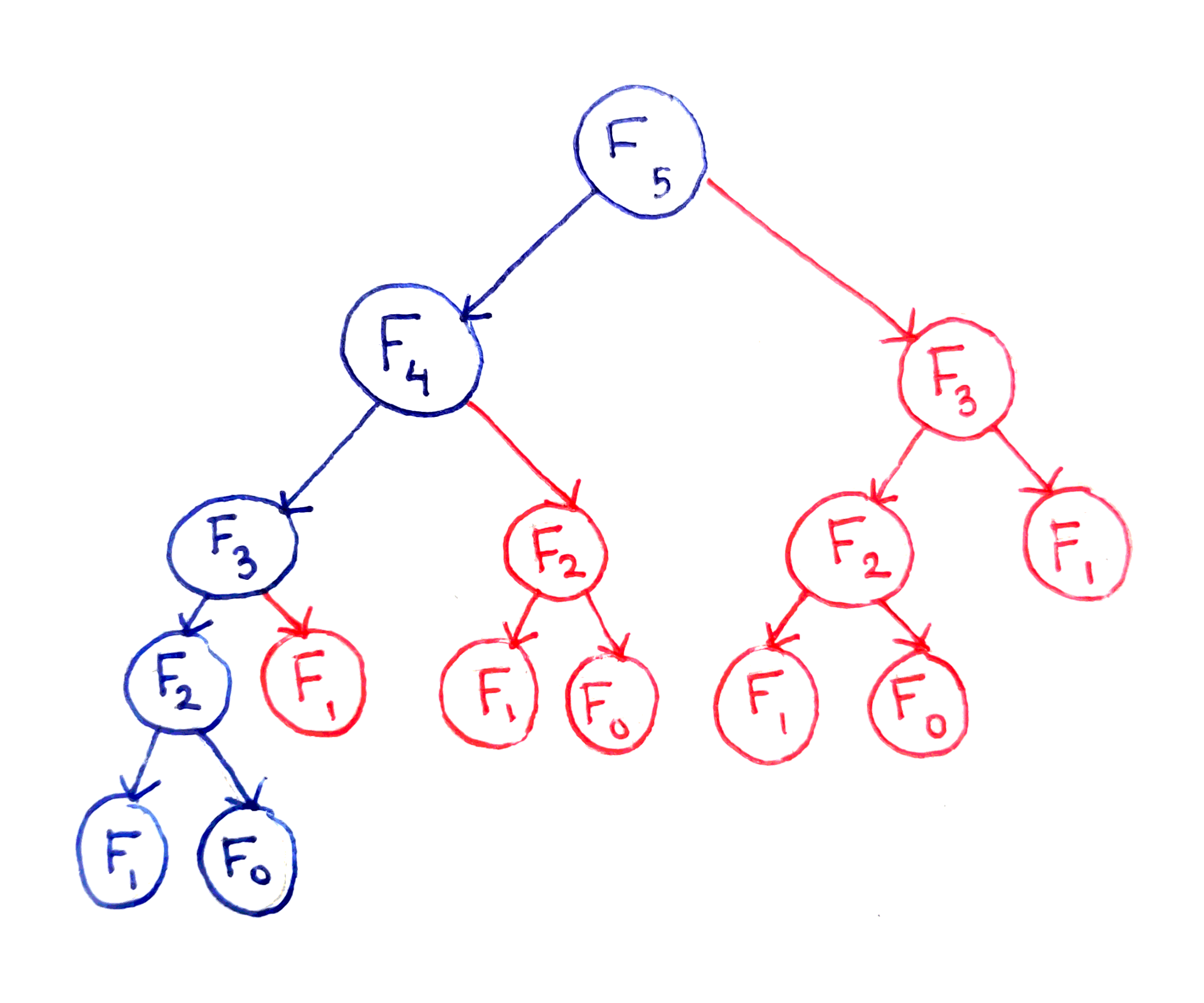
Bài toán dãy con tăng dài nhất

Thuật toán quy hoạch động gồm 3 bước:

  1. Tìm công thức đệ quy biểu diễn nghiệm tối ưu của bài toán lớn thông qua nghiệm tối ưu của các bài toán con
  2. Tổ chức dữ liệu lưu kết quả tính toán
  3. Dựa vào kết quả ghi nhận truy vết tìm ra nghiệm tối ưu

Tham khảo việc làm JavaScript tại Hồ Chí Minh trên TopDev

Áp dụng phương pháp quy hoạch động vào bài toán dãy con tăng dài nhất, chúng ta sẽ xác đinh công thức quy hoạch động như sau:

Đề bài: Cho dãy số A với n phần tử, yêu cầu tìm ra dãy con tăng dài nhất

A(i1), A(i2), … A(ik) thỏa mãn i1<i2<….<ik và A(i1)<A(i2)<….A(ik)

Gọi F(i) là dãy con tăng dài nhất kết thúc ở A(i), ta có công thức đệ quy:

F(1) = 1

F(i) = max(F(j) + 1) với j thỏa mãn điều kiện 1<=j<i và A(j)<A(i)

Kết quả đầu ra bài toán sẽ là giá trị lớn nhất của trong mảng F.

Ví dụ như sau:

Mảng A 1 11 2 10 4 5 2 1
Mảng F 1 2 2 3 3 4 2 1

Kết quả đầu ra cho ví dụ trên thì dãy con tăng dài nhất sẽ có độ dài = 4; mảng đầu ra sẽ là [1, 2, 4, 5]

Xem việc làm javascript đãi ngộ tốt trên TopDev

Triển khai code JavaScript

Source code tham khảo triển khai giải thuật dành cho bài toán dãy con tăng dài nhất bằng JavaScript các bạn có thể tham khảo dưới đây:

export default function dpLongestIncreasingSubsequence(sequence) {
  const lengthsArray = Array(sequence.length).fill(1);

  let previousElementIndex = 0;
  let currentElementIndex = 1;

  while (currentElementIndex < sequence.length) {
    if (sequence[previousElementIndex] < sequence[currentElementIndex]) {
      const newLength = lengthsArray[previousElementIndex] + 1;
      if (newLength > lengthsArray[currentElementIndex]) {
        lengthsArray[currentElementIndex] = newLength;
      }
    }

    previousElementIndex += 1;

    if (previousElementIndex === currentElementIndex) {
      currentElementIndex += 1;
      previousElementIndex = 0;
    }
  }

  let longestIncreasingLength = 0;

  for (let i = 0; i < lengthsArray.length; i += 1) {
    if (lengthsArray[i] > longestIncreasingLength) {
      longestIncreasingLength = lengthsArray[i];
    }
  }

  return longestIncreasingLength;
}

Giá trị trả về longestIncreasingLength là độ dài của dãy con lớn nhất thỏa mãn yêu cầu đề bài. Để lấy ra được giá trị mảng con, chúng ta cần triển khai thêm bước truy vết lấy từng phần tử từ dãy đầu vào theo thứ tự ngược lại của vòng lặp, các bạn có thể tự triển khai thêm nhé.

Chi phí thời gian thực hiện giải thuật này là O(n log n) với n là độ dài mảng đầu vào.

Kết bài

Như vậy qua bài viết này chúng ta đã cùng nhau tìm hiểu về bài toán về dãy con tăng dài nhất và cách giải quyết nó bằng thuật toán quy hoạch động cùng cách triển khai bằng ngôn ngữ lập trình JavaScript. Hy vọng bài viết hữu ích dành cho các bạn và hẹn gặp lại trong các bài viết tiếp theo của mình.

Tác giả: Phạm Minh Khoa

Có thể bạn quan tâm:

Hàng loạt việc làm IT hấp dẫn trên TopDev đang chờ bạn ứng tuyển..

RELATED ARTICLESMORE FROM AUTHOR