Thuật toán Brute Force và bài toán Trapping Rain Water

963

Thuật toán Brute Force hay còn được gọi là thuật toán vét cạn là một trong những giải thuật cơ bản trong lập trình mà mọi người thường xuyên sử dụng. Bài viết hôm nay chúng ta cùng nhau tìm hiểu về thuật toán này và áp dụng nó để giải quyết bài toán Trapping Rain Water nhé.

Thuật toán Brute Force

Thuật toán vét cạn (Brute Force) đúng như cái tên của nó sẽ thực hiện việc xét qua tất cả các trường hợp có thể xảy ra để tìm kiếm kết quả. Thuật toán này cho chúng ta một cách tiếp cận đơn giản, dễ hiểu, dễ nhận thấy nhất mặc dù nó không phải là cách tốt nhất.

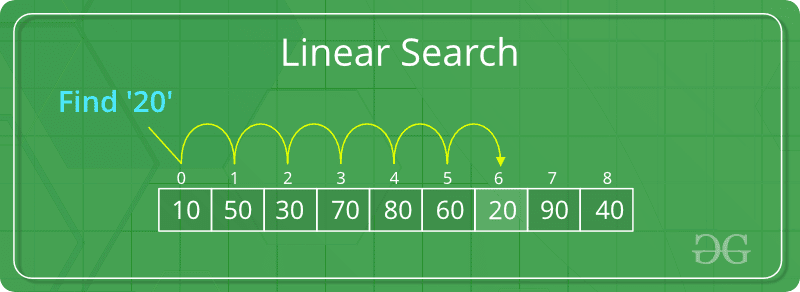
Thuật toán Brute Force

Linear Search (tìm kiếm tuyến tính) là một bài toán tiêu biểu của thuật toán vét cạn, với việc duyệt qua lần lượt các phần tử trong mảng cho đến khi tìm ra được giá trị cần tìm. Rõ ràng với việc duyệt qua tất cả các trường hợp có thể xảy ra thì Brute Force không được đánh giá cao về hiệu năng và không phù hợp để giải quyết các bài toán có quy mô lớn. Điều kiện tiên quyết để áp dụng Brute Force là cần xem xét đến case xấu nhất có thể là gì và thời gian cho đủ cho phép để thực hiện case đó không.

Mặc dù vậy đây vẫn là một thuật toán kinh điển cơ bản và rất hữu ích khi bạn chưa nghĩ ra được phương án nào tối ưu. Ngoài ra việc triển khai thuật toán cũng đơn giản giúp ít mắc lỗi hơn trong quá trình lập trình.

  Tìm hiểu về thuật toán đảo ngược chuỗi liên kết (Linked List)

  Thuật toán tham lam (Greedy Algorithm) – Thực hành với C++

Bài toán Trapping Rain Water

Bài toán: Cho một dãy số nguyên không âm height với giá trị phần tử trong mảng là chiều cao của các khối trụ tường giữ nước với độ rộng đều bằng 1. Hãy tính tổng diện tích các trũng nước sau khi mưa

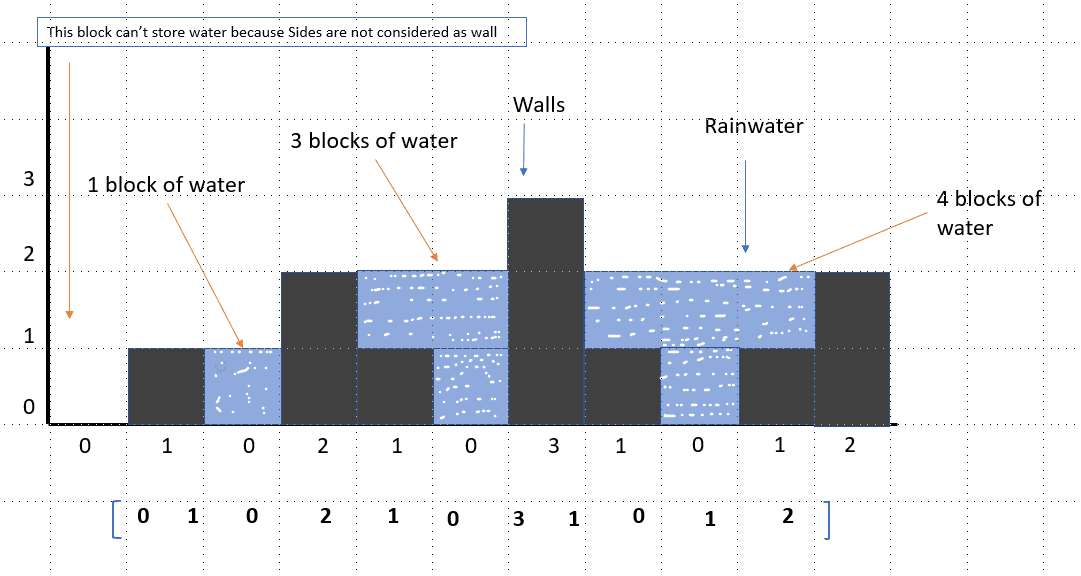
Bài toán Trapping Rain Water

  • Input: height = [0, 1, 0, 2, 1, 0, 3, 1, 0, 1, 2]
  • Output: 8

Như thể hiện trên hình vẽ, với các khối trụ tường (phần màu đen) được tạo ra theo giá trị mảng đầu vào thì sẽ chỉ có 3 vùng nước được giữ lại tương ứng với tổng khối nước là 1 + 3 + 4 = 8 (phần màu xanh tương ứng). 

Phân tích bài toán

Tại mỗi vị trí phần tử trong mảng, lượng nước có thể giữ được sẽ phụ thuộc vào chiều cao khối trụ tường của 2 bên trái phải của điểm đó. Ví dụ với phần tử thứ 6 trong hình trên (giá trị phần tử = 0); bức tường cao nhất ở phía bên trái của điểm đó có độ cao = 2 (phần tử thứ 4); và bức tường cao nhất ở phía bên phải của điểm đó có độ cao = 3 (phần tử thứ 7). Lượng nước giữ lại được tại node này sẽ chính là giá trị nhỏ hơn trong 2 giá trị trên trừ đi chiều cao của chính phần tử đó.

Với phân tích trên thì lời giải cho bài toán chính là việc duyệt qua từng vị trí của phần tử trong mảng, tại mỗi vị trí sẽ tính ra lượng nước giữ lại được; cuối cùng là tính tổng của tất cả giá trị trên sẽ cho ra lời giải của bài toán. Đây cũng chính là cách giải theo phương pháp vét cạn, tính toán hết các khả năng có thể xảy ra.

Tham khảo việc làm Front-End hấp dẫn trên TopDev

Triển khai thuật toán

  1. Khởi tạo giá trị trả về ans = 0
  2. Chạy vòng lặp mảng đầu vào từ trái sang phải và thực hiện:
    1. Khởi tạo giá trị max_left = 0 và max_right = 0
    2. Chạy vòng lặp từ phần tử hiện tại đến phần tử bắt đầu mảng và xác định max_left = max(max_left, height[j])
    3. Chạy vòng lặp từ phần tử hiện tại đến phần tử cuối của mảng và xác định max_right = max(max_right, height[j])
    4. Cộng thêm giá trị min(max_left, max_right) – height[i] vào ans

Độ phức tạp của thuật toán

Đối với mỗi phần tử của mảng, chúng ta cần thực hiện vòng lặp phần bên trái và phần bên phải, tương đương với việc duyệt qua mảng thêm 1 lần. Vì vậy độ phức tạp của thuật toán về mặt thời gian sẽ là O(n^2). Về bộ nhớ sử dụng thì độ phức tạp của thuật toán này chỉ là O(1).

Triển khai thuật toán bằng ngôn ngữ JavaScript

export default function trappingRainWater(height) {
  let ans = 0;

  for (let index = 0; index < height.length; index += 1) {
    let max_left = 0;
    for (let leftIndex = index - 1; leftIndex >= 0; leftIndex -= 1) {
      max_left = Math.max(max_left, height[leftIndex]);
    }

    let max_right = 0;
    for (
      let rightIndex = index + 1;
      rightIndex < height.length;
      rightIndex += 1
    ) {
      max_right = Math.max(max_right, height[rightIndex]);
    }

    const max_height = Math.min(max_left, max_right);
    if (max_height > height[index]) {
      ans += max_height - height[index];
    }
  }

  return ans;
}

Kết bài

Giải thuật vét cạn thường không phải là giải thuật tối ưu nhất là trong các bài toán cần xử lý với giá trị đầu vào có kích thước lớn. Mặc dù vậy nó sẽ tỏ ra tối ưu khi giá trị đầu vào có kích thước nhỏ, không cần quá chú trọng vào thời gian xử lý; ngoài ra đây là một thuật toán dễ triển khai, giảm bớt lỗi có thể xảy ra. Ngoài bài toán Trapping Rain Water ở trên thì Brute Force có thể áp dụng và triển khai được trong rất nhiều bài toán khác nhau và được xem như một cách tiếp cận cơ bản nhất trong lập trình. Hy vọng bài viết hữu ích dành cho bạn và hẹn gặp lại trong các bài viết tiếp theo của mình.

Tác giả: Phạm Minh Khoa

Xem thêm:

Tham khảo ngay việc làm IT mọi cấp độ trên TopDev!

RELATED ARTICLESMORE FROM AUTHOR