Công nghệ

Các thuật toán sắp xếp phổ biến trong JavaScript

27495

Bài viết được sự cho phép của tác giả Lưu Bình An

Chúng ta sẽ hiện thực các thuật toán này bằng JavaScript,.

Hàm helper để swap giá trị

function swap(arr, a, b) {
    let temp = arr[a];
    arr[a] = arr[b];
    arr[b] = temp;
}

Hàm để so sánh giá trị

const Compare = {
    LESS_THAN: -1,
    BIGGER_THAN: 1
};

function defaultCompare(a, b) {
    if (a === b) {
        return 0;
    }
    return a < b ? Compare.LESS_THAN : Compare.BIGGER_THAN;
}

Bubble Sort

Tình huống tốt nhất: độ phức tạp = O(N) (đi qua đúng n phần tử)
Tình huống xấu nhất: độ phức tạp = O(N^2) (đi qua n mũ 2 phần tử)

Cái này rất ít xài trong thực tế, chỉ để dạy và học, vì nó chậm nhất so với các thuật toán khác.

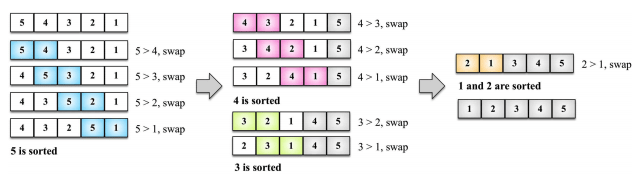
Ý tưởng là sẽ so sánh 2 phần tử liền kề, hoán đổi vị trí cho phù hợp

function bubbleSort(arr, compare = defaultCompare) {
    const { length } = arr;
    for (let i = 0; i < length; i++) {
        for (let j = 0; j < length - 1 - i; j++) { // refer to note below
            if (compare(arr[j], arr[j + 1]) === Compare.BIGGER_THAN) {
                swap(arr, j, j + 1);
            }
        }
    }
    return arr;
}

Để hình dung thuật toán này, bạn có thể nghiên cứu cái hình mô tả bên dưới

Selection Sort

Không phân biệt tính huống tốt hay xấu gì cả, nó luôn có độ phức tạp = O(N^2)

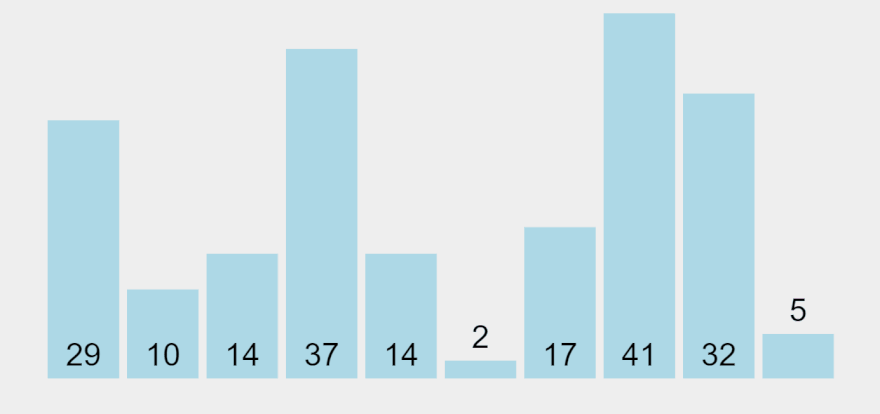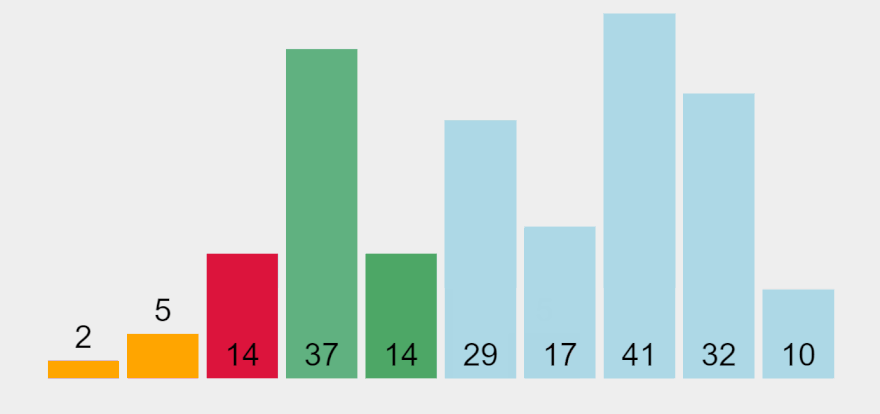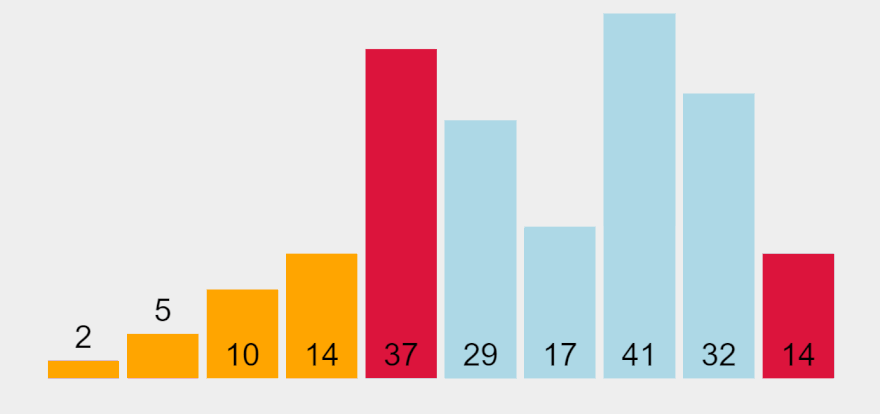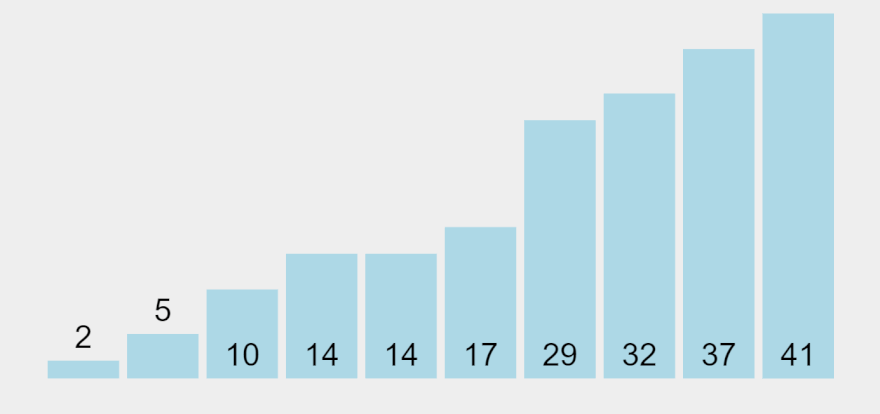
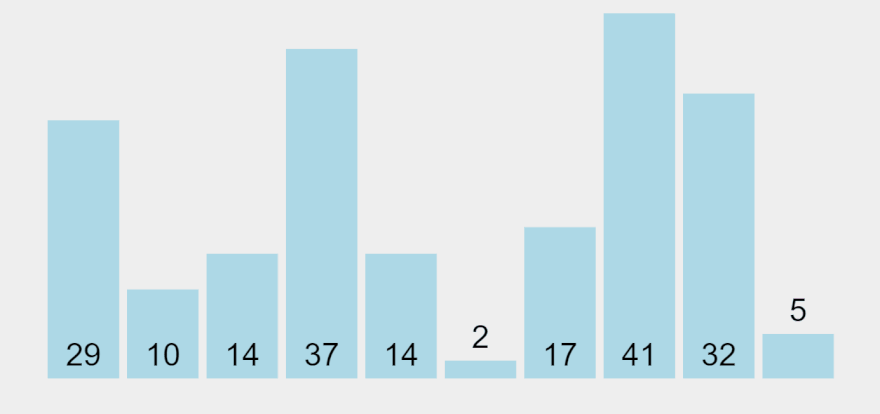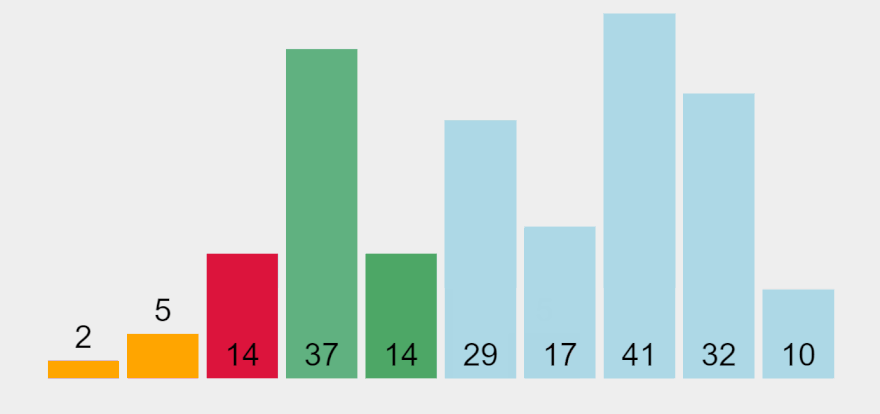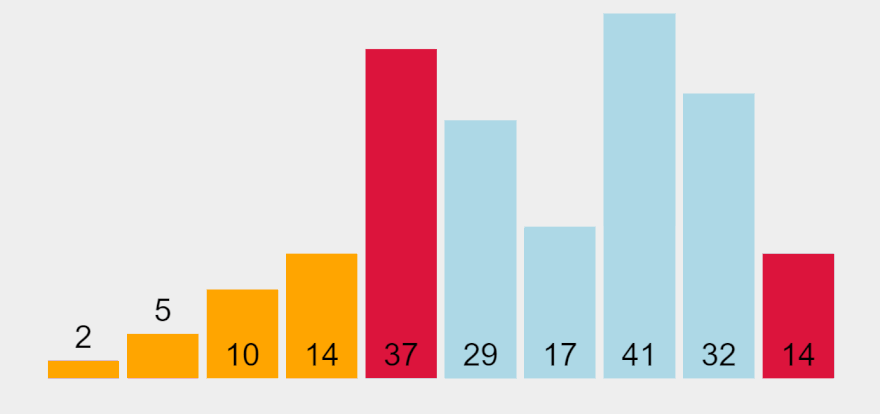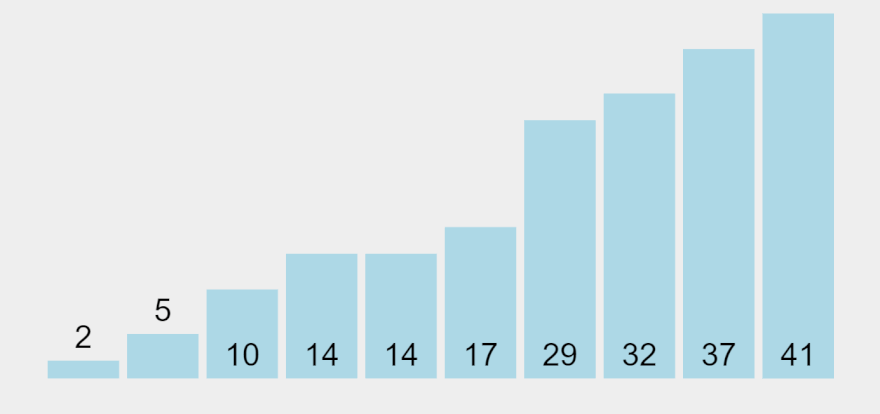
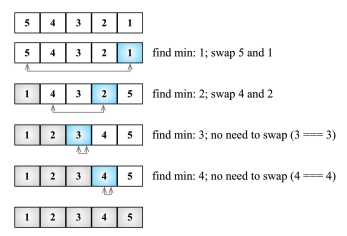
Ý tưởng của thuật toán là tìm ra giá trị nhỏ nhất trong đám, rồi đưa nó về vị trí đầu tiên, lặp lại cho các phần tử kế tiếp.

function selectionSort(arr, compare = defaultCompare) {
    const { length } = arr;
    let minIndex;
    for (let i = 0; i < length - 1; i++) {
        minIndex = i;
        for (let j = i; j < length; j++) {
            if (compare(arr[minIndex], arr[j]) === Compare.BIGGER_THAN) {
                minIndex = j;
            }
        }
        if (i !== minIndex) {
            swap(arr, i, minIndex);
        }
    }
    return arr;
}

Insertion Sort

Tình huống tốt nhất: độ phức tạp = O(N)
Tình huống xấu nhất: độ phức tạp = O(N^2)

Thuật toán này nó sẽ tạo ra mảng mới, tìm và chèn từng phần tử một vào đúng thứ tự. Sẽ như sau

Cứ coi như phần tử đầu tiên là đúng vị trí
Lấy phần tử đầu tiên này so sánh với phần tử tiếp theo, nó có 2 tình huống một là ở yên vị trí đang ở, hay là chúng ta chèn phần tử thứ 2 vào trước phần tử đầu.
Lặp lại tương tự

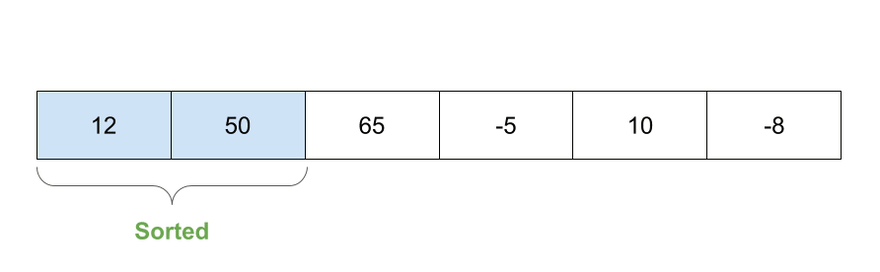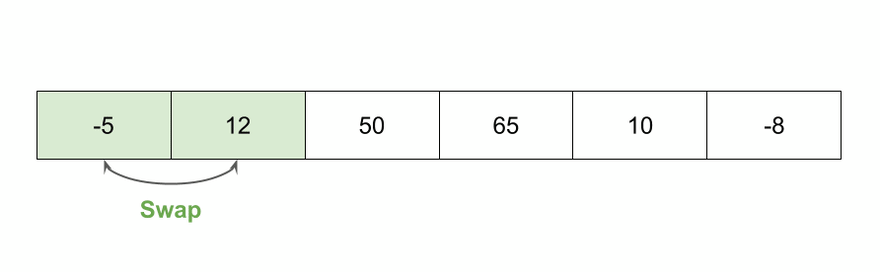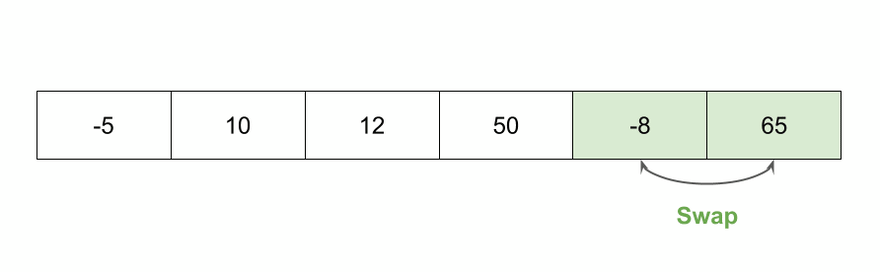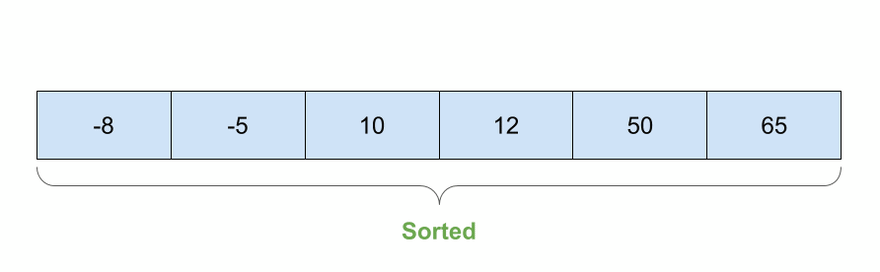
function insertionSort(arr, compare = defaultCompare) {
    const { length } = arr;
    let temp;
    for (let i = 1; i < length; i++) {
        let j = i;
        temp = arr[i];
        while (j > 0 && compare(arr[j - 1], temp) === Compare.BIGGER_THAN) {
            arr[j] = arr[j - 1];
            j--;
        }
        arr[j] = temp;
    }
    return arr;
}

Merge Sort

Độ phức tạp cố định: O(N Log N)

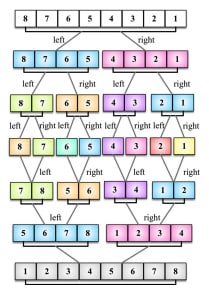
Là thuật toán chia để trị, chi nhỏ các phần tử ban đầu ra thành các nhóm nhỏ hơn để dể xử lý từng cụm

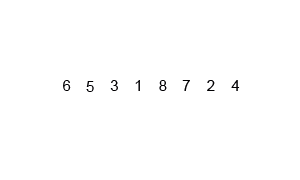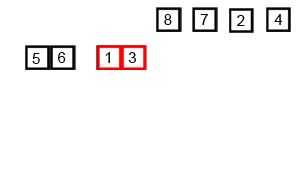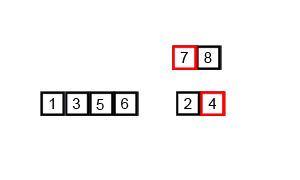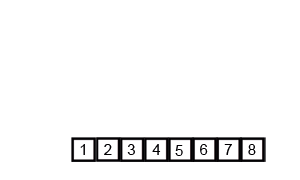
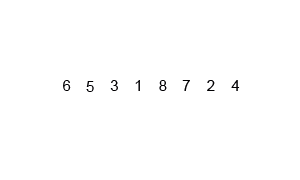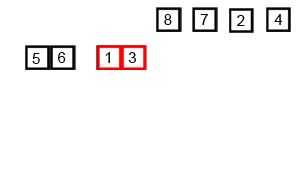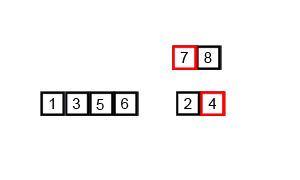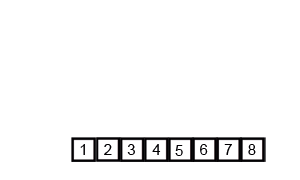
function mergeSort(arr, compare = defaultCompare) {
    if (arr.length > 1) {
        const { length } = arr;
        const middle = Math.floor(length / 2);
        const left = mergeSort(arr.slice(0, middle), compare);
        const right = mergeSort(arr.slice(middle, length), compare);
        arr = merge(left, right, compare);
    }
    return arr;
}

function merge(left, right, compare) {
    let i = 0;
    let j = 0;
    const result = [];
    while (i < left.length && j < right.length) {
        result.push(compare(left[i], right[j]) === Compare.LESS_THAN ? left[i++] : right[j++]);
    }
    return result.concat(i < left.length ? left.slice(i) : right.slice(j));
}

Quick sort

Tình huống tốt nhất: độ phức tạp = O(N Log N)
Tình huống xấu nhất: độ phức tạp = O(N^2)

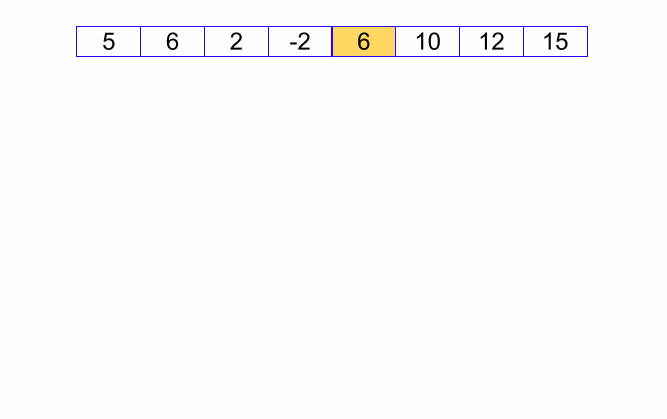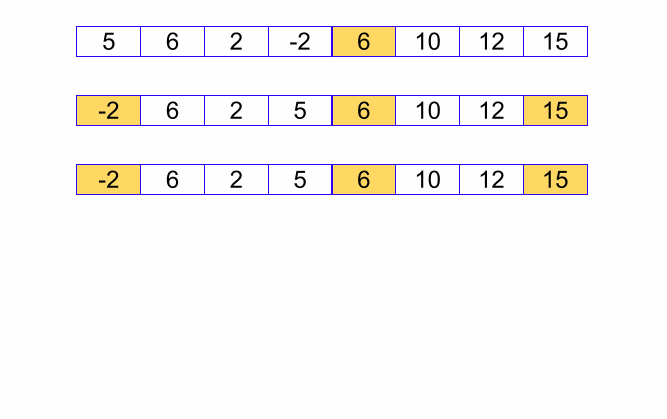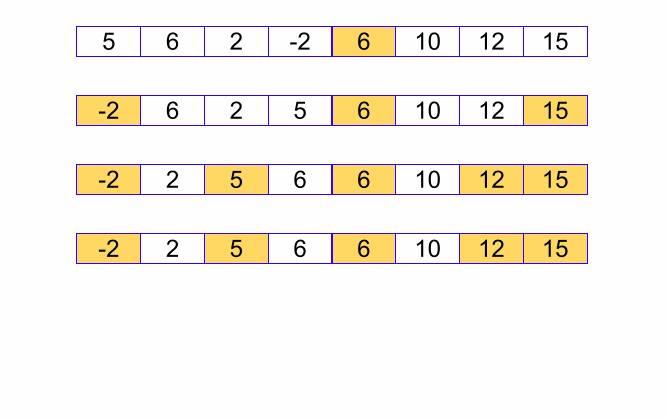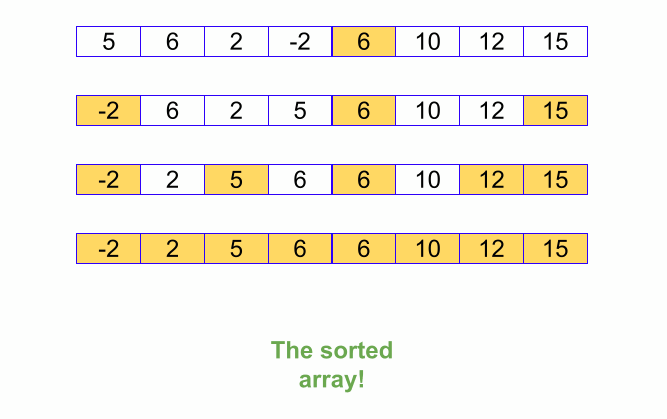
Đây là thuật toán được sử dụng nhiều nhất, vẫn là phương pháp chia để trị

Có thể xem lại bài giới thiệu về Quick Sort của mình

function quickSort(arr, compare = defaultCompare) {
    return quick(arr, 0, arr.length - 1, compare);
}

function quick(arr, left, right, compare) {
    let i;
    if (arr.length > 1) {
        i = partition(arr, left, right, compare);
        if (left < i - 1) {
            quick(arr, left, i - 1, compare);
        }
        if (i < right) {
            quick(arr, i, right, compare);
        }
    }
    return arr;
}

function partition(arr, left, right, compare) {
    const pivot = arr[Math.floor((right, left) / 2)];
    let i = left;
    let j = right;

    while (i <= j) {
        while (compare(arr[i], pivot) === Compare.LESS_THAN) {
            i++;
        }
        while (compare(arr[j], pivot) === Compare.BIGGER_THAN) {
            j--;
        }
        if (i <= j) {
            swap(arr, i, j);
            i++;
            j--;
        }
    }
    return i;
}

Bucket Sort

Tình huống tốt nhất: độ phức tạp = O(N + k)
Tình huống xấu nhất: độ phức tạp = O(N^2)

Ý tưởng là sẽ chia đôi thành 2 mảng, rồi trên từng mảng đó, áp dụng một thuật toán sắp xếp trên đó, như insertion sort

function bucketSort(arr, bucketSize) {
    if (arr.length < 2) {
        return arr;
    }
    // create buckets and distribute the elements
    const buckets = createBuckets(arr, bucketSize);
    // sort the buckets using insertion sort and add all bucket elements to sorted result 
    return sortBuckets(buckets);
}

function createBuckets(arr, bucketSize) {
    // determine the bucket count
    let min = arr[0];
    let max = arr[0];
    for (let i = 1; i < arr.length; i++) {
        if (arr[i] < min) {
            min = arr[i];
        } else if (arr[i] > max) {
            max = arr[i];
        }
    }
    const bucketCount = Math.floor((max - min) / bucketSize) + 1;

    // initialize each bucket (a multidimensional array)
    const buckets = [];
    for (let i = 0; i < bucketCount; i++) {
        buckets[i] = [];
    }

    // distribute elements into buckets
    for (let i = 0; i < arr.length; i++) {
        const bucketIndex = Math.floor((arr[i] - min) / bucketSize);
        buckets[bucketIndex].push(arr[i]);
    }
    return buckets;
}

function sortBuckets(buckets) {
    const sortedArr = [];
    for (let i = 0; i < buckets.length; i++) {
        if (buckets[i] != null) {
            insertionSort(buckets[i]); // quick sort is another good option
            sortedArr.push(...buckets[i]);
        }
    }
    return sortedArr;
}

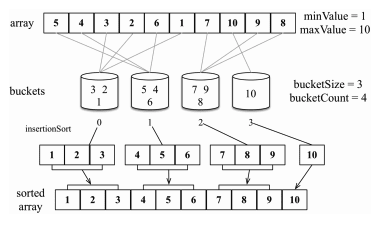
Lưu ý bucket sort chạy tốt nhất khi có thể chia đều các phần tử cho các bucket, việc chia thành 2 bucket cũng không bắt buộc, có thể chia nhiều hơn nếu số lượng phần tử nhiều

Bài viết gốc được đăng tải tại vuilaptrinh.com

Có thể bạn quan tâm:

Xem thêm các việc làm JavaScript hấp dẫn tại TopDev